Matrix and Matrix Editor Tutoral
This is supposed to be a brief tutorial to introduce you to basic 3D
transformation matrices and the matrix stack editor in the newer (>=1.5)
versions of my modification to jonwil's RCT3 importer.
Contents
Introduction On Used Terms
In this section I'll give a short introduction on the terms you'll need to
understand 3D matrix transformations. I'll start with the mathematical
definition and then try to explain in easy words what it means and how it
applies to 3D objects and their manipulation.
- Coordinate System
- A system for specifying points using coordinates measured in some
specified way. The simplest coordinate system consists of coordinate
axes oriented perpendicularly to each other, known as Cartesian
coordinates. Depending on the type of problem under consideration,
coordinate systems possessing special properties may allow particularly
simple solution.
Weisstein, Eric W. "Coordinate System." From
MathWorld--A Wolfram Web Resource.
In short, a coordinate system is a way to describe a point in space. As we
want to work with 3D objects, we use a three dimensional coordinate system
with three axes (sing. axis) called x, y and z. We also use a
cartesian
coordinate system, which means that all axes are, like stated above,
perpendicular to each other (If you're not familar with the term, it means
they form right (90 degree) angles with each-other).
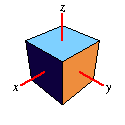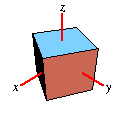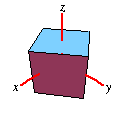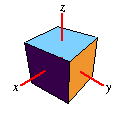
What needs further explanation are the terms
right-handed and
left-handed coordinate system. This arises from the fact that there
are two possible ways to form a cartesian coordinate system in 3D space.
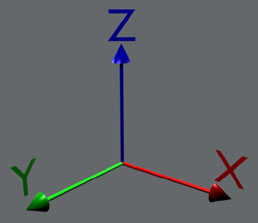
Whether a coordinate system is left- or rightshanded can be easily determined
with syou guessed it- your hand. Using your
right hand,
point the
thumb in the direction of the x-axis and your
index finger in the direction of the y-axis. If you now can
point your
middle finger in the direction of the z-axis
without hurting yourself (or overbending if you're flexible enough :-) ),
it's a
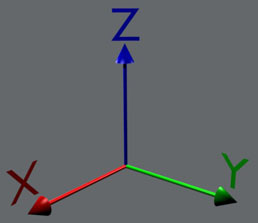
right-handed coordinate system. Here are two pictures
to practice:
|
|
| Left-handed coordinate system |
Right-handed coordinate system |
Which way is up is only a matter of perspective, not a real difference in
coordinate systems :-)
Why do we need to discuss this? Many modelers (eg Blender) use a right-handed
z-up coordinate system. This is the mathematical standart. It probably
originates from 2D drawing. If you plot on a paper you use a 2D coordinate
system where usually the x-axis points to the right and the y-axis points to
the top of the sheet. If you now envision 3D space to "pop-out" of the paper
along a z-axis you arrive at a right-handed, z-up system.
In 3D games, things are different. First, envision the 2D drawing on your
screen. To switch to 3D, treat your screen as a window. Now the z-axis
streches out into the "depth" of the screen. Jiggle your fingers, and you'll
see that this constitutes a left-handed, y-up coordinate system, which is the
standart in 3D gaming. RCT3 uses such a system.
This is the reason I added the fixup to the importer. If you model in a
right-handed z-up system and import into RCT3, your model will end up lying
on the side, being burried half in the earth and mirrored.
(Note: MilkShape uses a right-handed, y-up coordinate system. Don't ask me
why.)
- Vertex (pl. vertices)
- A vertex is a special point of a mathematical object, and is usually
a location where two or more lines or edges meet. Vertices are most
commonly encountered in angles, polygons, polyhedra, and graphs. Graph
vertices are also known as nodes.
Weisstein, Eric W. "Vertex." From
MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/Vertex.html
In short easy words, for us a vertex is a point in three-dimensional space.
It's the basic building block of 3D objects.
To get a full 3D object, vertices are connected by edges that form
faces (sometimes also called
Polygons or
Polys).
Current 3D graphic cards use only triangular faces, therefore faces are often
also called
triangles or
tris. Some 3D modelers can also
work with 4 vertex faces (
quads) or even larger ones, but these need
to be converted to triangles before you can use them for 3D games. This
usually happens automatically when you save to a file format that only
supports triangular faces. In some cases you might want to do this manually
to get a certain look.
I will not discuss edges and faces further because they are not really
relevant for 3D transformation matrices.
- Vector (pl. vectors)
- A vector is formally defined as an element of a vector space. In the
commonly encountered vector space Rn (i.e., Euclidean
n-space), a vector is given by n coordinates and can be specified as (A1, A2, ...,
An). Vectors are sometimes referred to by the
number of coordinates they have, so a 2-dimensional vector (x1,x2) is often called a
two-vector, an n-dimensional vector
is often called an n-vector, and so
on.
Weisstein, Eric W. "Vector." From
MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/Vector.html
So far the formal definition. I cited this mainly to show you that by
definition a vertex and a vector are different things, while in 3D
programming slang they are often used as the same. Formally a vector is an
arrow, ie it has a direction and a length. In 3D space it has three
coordinates.
I'll stop here so I don't confuse you :-) For our purpose, you can safley
assume that a vector and a vertex are the same. If you want to be more
precise, imagine the vector to be the arrow that points from the origin to
the vertex.
- Matrix (pl. matrices)
- A matrix is a concise and useful way of uniquely representing and
working with linear transformations. In particular, for every linear
transformation, there exists exactly one corresponding matrix, and
every matrix corresponds to a unique linear transformation. The matrix,
and its close relative the determinant, are extremely important
concepts in linear algebra, and were first formulated by Sylvester and
Cayley.
Weisstein, Eric W. "Matrix." From
MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/Matrix.html
To sum it up for our purpose, a matrix is a way to move around vertices in a
certain way. Usually a matrix in 3D space would be 3 x 3 big. As you will see
later, we'll use 4 x 4 matrices, which makes linear translation (= linear
movement) much easier.
To transform a vertex (or vector in this case) it needs to be multiplied with
the matrix. The exact procedure is beyond this brief introduction, but what
you should know is, that it's mathematically impossible to multiply a 3D
vector with a 4D matrix. To apply a 4D matrix we need a small trick. We just
make the vector 4D by adding a fourth coordinate which we set to 1 (That's
actually what makes the translation matrices work).
So why are matrices so convenient for 3D transformations? The reason is that
you can merge several matrices into one, that in one step does all the
transformations of the ones you merged. The mathematical operation behind
this is called a
matrix multiplication and, like the vector-matrix
multiplication, differs from the multiplication of numbers. The most
important difference is that matrix multiplication is not
commutative. This
means the order of multiplication
does matter, if
A and
B are matrices,
A•B is
not equal to
B•A. The matrix that results fom the multiplication
A•B does the same as applying
A first and then
B. If you
think a bit about it, it should be clear that in many cases you'll get a
different result if you do it the other way around.
Transformation Matrix Types
All the transformation matrices I'll explain now work with the origin as
center of operation. This doesn't matter for translation matrices, but is
important for rotation and scaling matrices (see there).
Translation
|
| 1.0 0.0 0.0 0.0 |
| 0.0 1.0 0.0 0.0 |
| 0.0 0.0 1.0 0.0 |
| x y z 1.0 |
|
Moves your object by
x, y, z in the respective direction.
Rotation
| Around X-Axis |
Around Y-Axis |
Around Z-Axis |
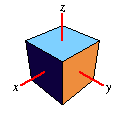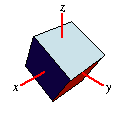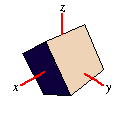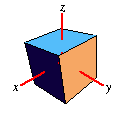
|
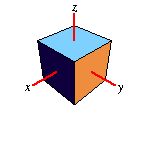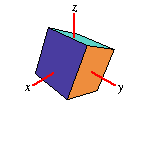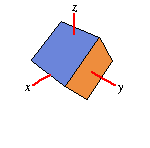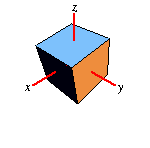
|
|
|
| 1.0 0.0 0.0 0.0 |
| 0.0 cos(a) -sin(a) 0.0 |
| 0.0 sin(a) cos(a) 0.0 |
| 0.0 0.0 0.0 1.0 |
|
| cos(a) 0.0 sin(a) 0.0 |
| 0.0 1.0 0.0 0.0 |
| -sin(a) 0.0 cos(a) 0.0 |
| 0.0 0.0 0.0 1.0 |
|
| cos(a) -sin(a) 0.0 0.0 |
| sin(a) cos(a) 0.0 0.0 |
| 0.0 0.0 1.0 0.0 |
| 0.0 0.0 0.0 1.0 |
|
| Weisstein, Eric W. "Rotation Matrix." From
MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/RotationMatrix.html |
Rotates your object by
a degrees around the respective axis. As
stated above, rotation is around the origin. If you need to rotate around a
different point, translate from that point to the origin, rotate and
translate back. This is what the "Set Origin to" button in the matrix editor
does automatically for you.
Scale
|
| Sx 0.0 0.0 0.0 |
| 0.0 Sy 0.0 0.0 |
| 0.0 0.0 Sz 0.0 |
| 0.0 0.0 0.0 1.0 |
|
Scales your object by
Sx, Sy, Sz in the respective direction from
the Origin. This means that if your object is away from the origin, the
distance is scaled as well and your object moves away from it. If you use a
negative factor, the object is mirrored in the respective direction as well
as scaled.




